Digit Image Process-直方图均衡化

发表于 2022-04-16 更新于 2024-12-13 分类于 DIP

直方图(Histogram)

定义图像灰度级为，其中，则未归一化的直方图定义为

$\begin{equation} h(r_{k})=n_{k} \end{equation}$

其中$n{k} $是图像在灰度级$ r{k}$的像素数量，归一化的直方图定义为

$\begin{equation} p(r_{k})=\frac{h(r_{k}}{MN}=\frac{n_{k}}{MN} \end{equation}$

其中和是图像的长和宽

直方图均衡化(Histogram Equalization)

直方图均衡化是一种强度转换映射，这种映射需要满足以下两点条件

在上是单调递增的
在上满足

单调递增是为了避免映射过程出现像素值的反转，更苛刻条件是严格单调递增，因为单调递增存在多对一的映射关系，如果要求从直方图均衡化转换回来，单调递增的多对一映射关系是有问题的，必须使用严格单调递增

直方图均衡化的目的是通过某种强度变换函数，使得变换后的图像灰度级均匀分布，展现更多细节和动态范围。图像的强度可以看作是在范围
内的随机变量。定义$p{r}(r) $和$ p{s}(s) $分别表示变换前后图像的强度概率密度函数。在概率论中，如果$ p{r}(r) $和$ T(r) $是已知的，且$ T(r) $在整个范围内连续可微，那么$ p{r}(r) $到$ p_{s}(s)$的映射可定义为

$\begin{equation} p_{s}(s) = p_{r}(r)\left|\frac{dr}{ds}\right| \end{equation}$

给出如下变换函数

$\begin{equation} s = T(r) = (L-1)\int_{0}^{r}p_{r}(\omega)d\omega \end{equation}$

积分部分是随机变量的累积分布函数(CDF)。由于PDF总为正，积分是递增的，满足条件1。当积分上限时，积分值为1，因此最大值为，
满足条件2。现在来推导一下，以下推导用到了莱布尼兹法则：定积分对其上限值的导数等于被积函数在上限处的值

$\begin{equation} \frac{ds}{dr} = \frac{dT(r)}{dr} \\ = (L-1)\frac{d}{dr}\int_{0}^{r}p_{r}(\omega)d\omega \\ = (L-1)p_{r}(r) \end{equation}$

将结果带回到变换中

\begin{equation}
p{s}(s) = p{r}(r)\left|\frac{dr}{ds}\right| \
= p{r}(r)\left|\frac{1}{L-1}p{r}(r)\right|\
= \frac{1}{L-1}
\end{equation}

可以看到，经过这个变换函数，变换后的图像概率密度函数在每个灰度级概率分布均匀

对于离散变量，可以使用求和来代替连续变量中的积分

\begin{equation}
s{k} = T(r{k}) = (L-1)\sum{j=0}^{k}p{r}(r_{j}) k=0,1,2,…,L-1
\end{equation}

直方图匹配

直方图均衡化由于结果的可预测性以及实现较为简单，在自动增强中是一个好的选择。但是有些应用场景中并不适合，尤其是期望经过处理后的图像直方图是某种特定分布时。生成具有特定直方图分布的方法叫做直方图匹配

如何将一个直方图分布变换到任意分布呢？假定期望的目标分布图像为，根据直方图均衡化的定义，同样也存在到的均衡化映射，定义为

\begin{equation}
S = G(z) = (L-1)\int{0}^{z}p{z}(v)dv
\end{equation}

那么可以得到从到的关系

由以上公式推断，可以看出，得到一个指定强度分布的图像可以通过如下步骤

从输入图像得到强度等级的PDF
使用目标分布的PDF得到G(z)
计算反变换z=G^{-1}(z)
通过输入图像得到均衡化的输出图像，并对均衡化输出图像的每个像素值进行z=G^{-1}(s)的逆变换映射

在连续变量中，逆变换并不好求得，但是在离散变量的处理中，实际上是不需要计算的，因为在进行映射时，所有强度等级的变换都记录在一个映射表中，逆映射时只需要从表中找出最接近的索引位置即可

例如以下例子中，映射数组tab将强度等级0~7映射到1,2,2,3,4,5,5,6，tab=[1,2,2,3,4,5,5,6]。要从5这个强度等级逆变换到映射前的强度等级，因为tab[5]和tab[6]都为5，选取最小的index=5就是逆变换后的值

Python Code

import cv2 as cv
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt

读取并显示图像信息

im = Image.open('images/02.tif').convert('L')
pixels_nr = im.width * im.height
pixels_max = 256
im.show()

直方图计算函数

def histogram(im):
    hist = np.zeros((pixels_max))
    data = np.array(im)
    for i in range(data.shape[0]):
        for j in range(data.shape[1]):
            v = data[i][j]
            hist[v] += 1
    return hist

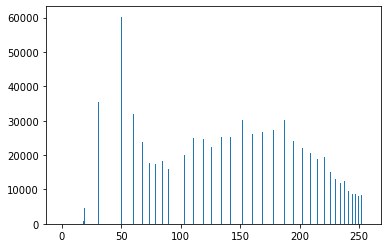
绘制直方图

1 2	hist = histogram(im) plt.bar(range(len(hist)), hist)

直方图均衡化函数

def histogram_equalization(im):
    r_data = np.array(im)
    # calculate hist
    hist = histogram(im)
    # calculate pdf
    pdf = hist / pixels_nr
    # calculate cdf
    cdf = pdf.cumsum()
    # generate map
    pmap = cdf * (pixels_max - 1)
    pmap = pmap.astype(np.uint8)
    # create new image
    s_data = np.zeros((r_data.shape[0], r_data.shape[1]), dtype=np.uint8)
    # mapping input image to new image
    s_data = pmap[r_data]
    return Image.fromarray(s_data)

进行直方图均衡化处理

1 2	out = histogram_equalization(im) out.show()

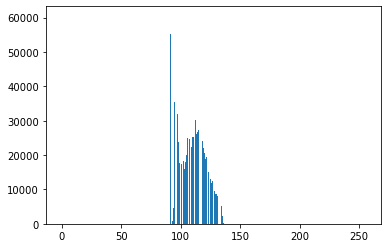
绘制均衡化后的图像直方图分布

1 2	out_hist = histogram(out) plt.bar(range(len(out_hist)), out_hist)