优先队列

发表于 更新于 分类于

普通的队列是一种FIFO结构，在优先队列(PriorityQueue)中，数据存在优先级，在进行出队操作时，具有最大(MaxPriorityQueue)或最小(MinPriorityQueue)优先级的元素最先出队。在很多应用场景中，都需要这种对数据进行有序处理或者按照优先级处理的方式

优先队列的应用很广泛，最常见的是进行任务调度，当有多个任务都需要处理的时候，为不同的任务划分优先级，并分别调度；优先队列还可以开发图搜索算法、数据压缩算法等

实现

优先队列的实现有很多方式，例如链表和数组。利用二叉堆来实现优先队列是一种较为高效的做法

结构 入队 出队最大元素
有序数组 N 1
无序数组 1 N
堆 logN logN

二叉堆实现的优先队列能够保证在插入和删除两个维度都较快

二叉堆

二叉堆是一组能够用堆有序的完全二叉树排列的元素，并在数组中按照层级存储

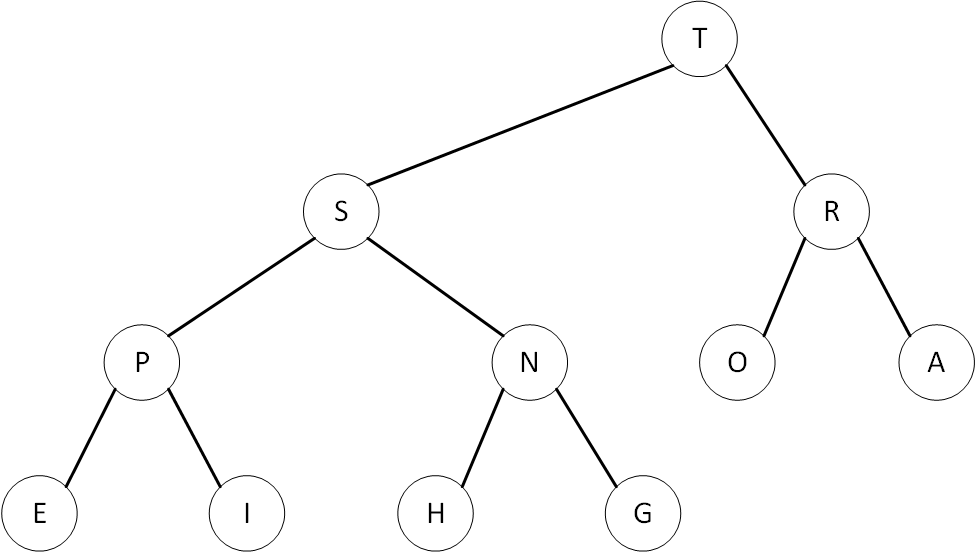
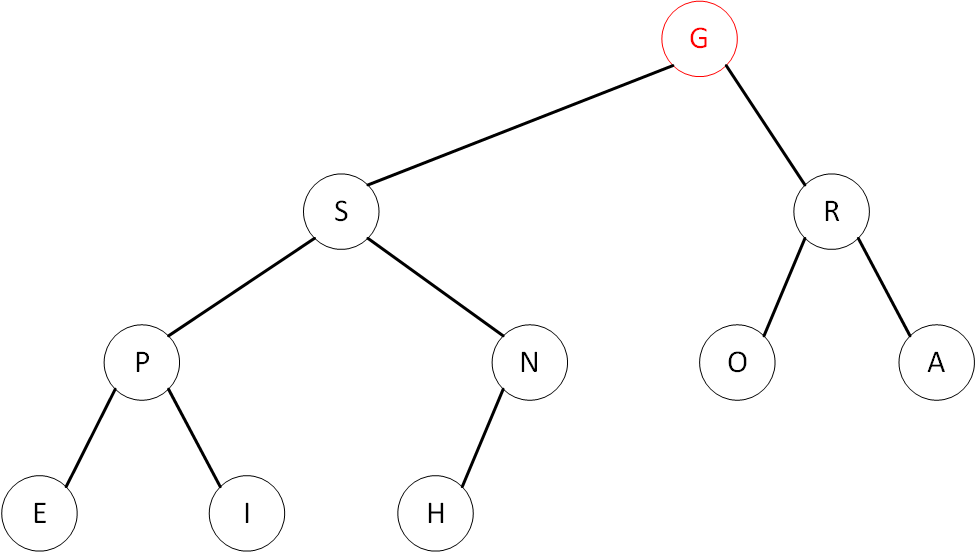
可以用下图来表示一个二叉堆

假设字幕A~Z表示的数值依次增大，则上图表示的是一个最大二叉堆(大根堆)，根节点”T”最大，二叉堆中任意子节点的数值不大于父节点数值

二叉堆有以下特性

  • 位置为k的节点父节点位置为k/2，两个子节点位置分别为2k和2k+1

  • 大小为N的完全二叉树高度为logN

以上性质决定了二叉堆在进行遍历或者搜索的路径是跳跃层级的，无论是插入还是删除操作，由于树高最大logN，因此操作的复杂度最大也为logN

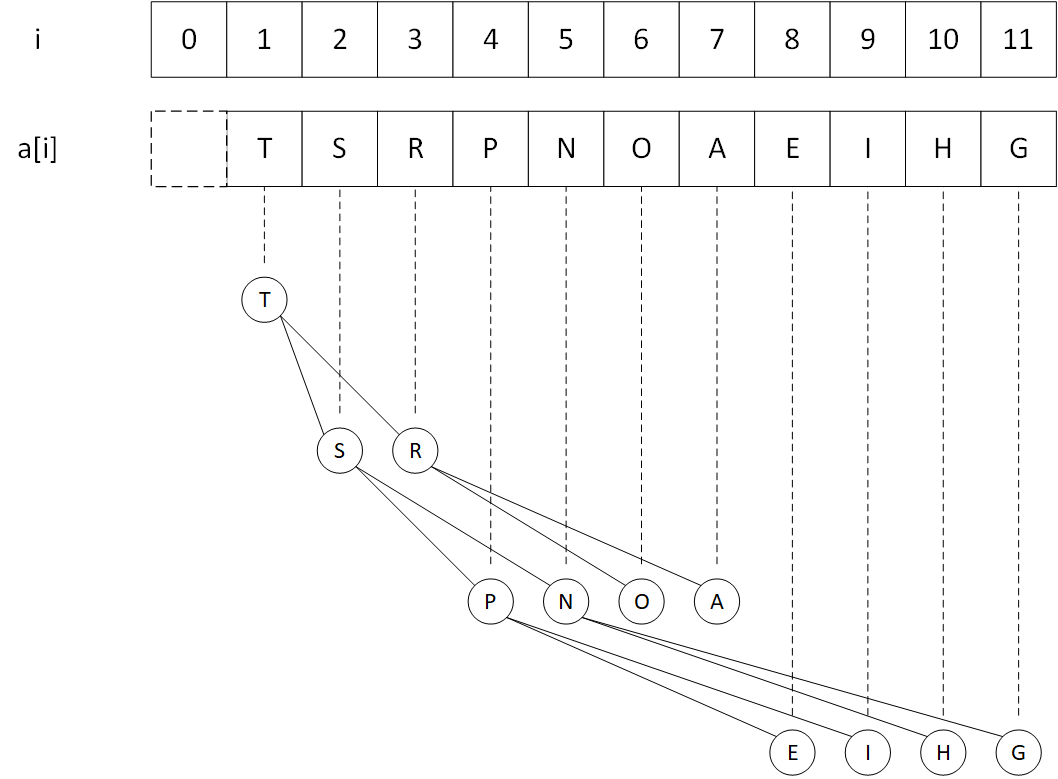
数组实现二叉堆

使用数组实现二叉堆是非常高效的，二叉堆中元素的位置和数组索引的关系可以用下图表示

使用数组实现二叉堆，仅利用数组索引就可以沿着树上下移动，非常便利。要注意为了编程时父子位置关系的统一性，数组的第一个位置不使用

在对堆进行操作时，会首先进行一些简单的改动，例如插入时先将元素插入到堆底，或者删除时先删除堆顶元素，这样会打破原有堆的有序状态，然后再将堆恢复有序状态(堆的有序化)。本文以最大优先队列为例，对堆的有序化操作进行说明

有序化需要用到两个辅助函数：比较(less)和交换(exch)。less函数是为了实现优先队列的泛化，希望实现的优先队列是一种泛型数据结构，而非某一种特定的数据结构，因此对于某一种具体的数据结构和类型，需要提供对应的比较函数”compare”，例如字符串String、文件File、时间Time等；交换两个元素是优先队列中使用非常频繁的操作，因此提取为单独的函数。以下是less和exch的伪代码

1
2
3
4
5
6
7
8
9
10
11
boolean less(array, compare, i, j)
{
    return compare(array[i], array[j]);
}

void exch(array, i, j)
{
    temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

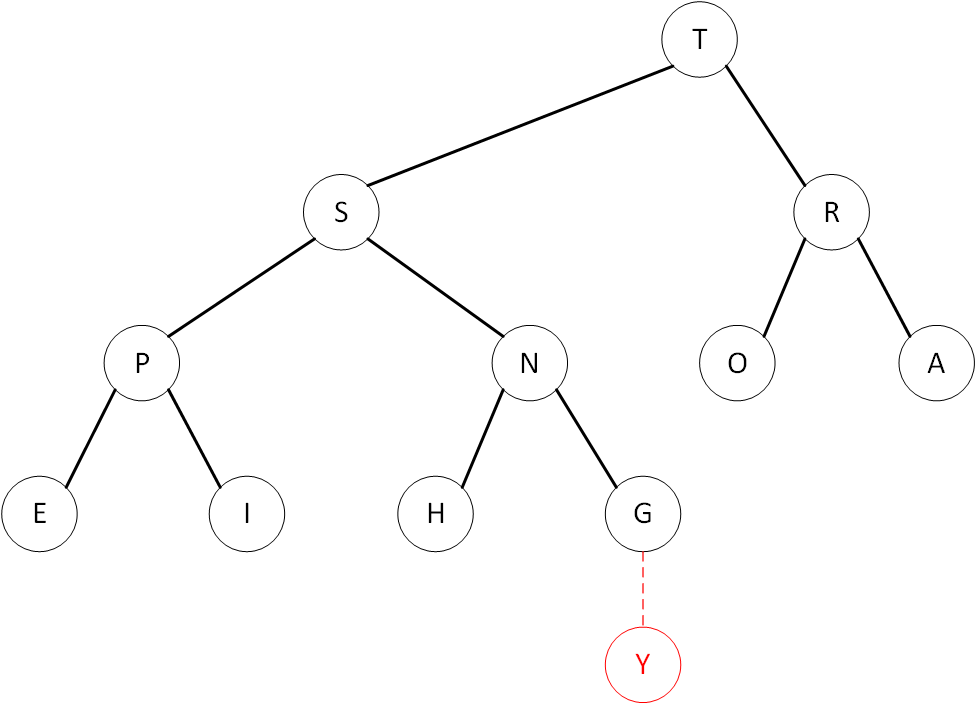
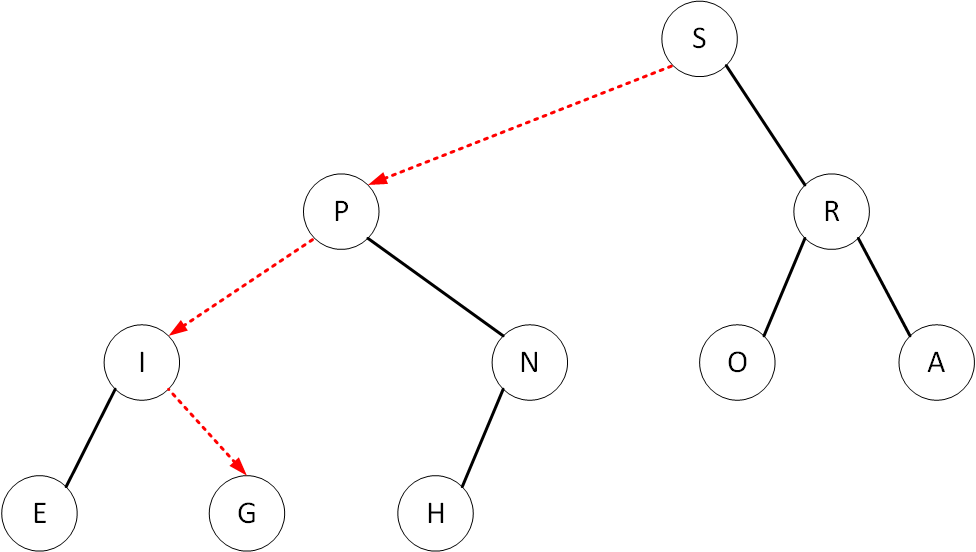
上浮(swim)

当插入一个元素到堆底后，如果该元素比其父节点更大，就需要通过上浮操作来对堆进行有序化。例如在G节点下向堆中插入元素”Y”

“Y”元素只需要一遍一遍的与其父节点进行比较，并交换它们的位置，当”Y”元素到达合适的位置时，整个堆就变得有序了

整个过程是插入元素不断地向上”浮动“，不在上浮路径上的元素都保持不变。有序化后部分元素的所在层数会发生变化。上浮的伪代码如下

1
2
3
4
5
6
7
8
// k: new item's index
void swim(k)
{
    while ((k>1) && less(k/2,k)) {
        exch(k/2, k);
        k = k/2;
    }
}

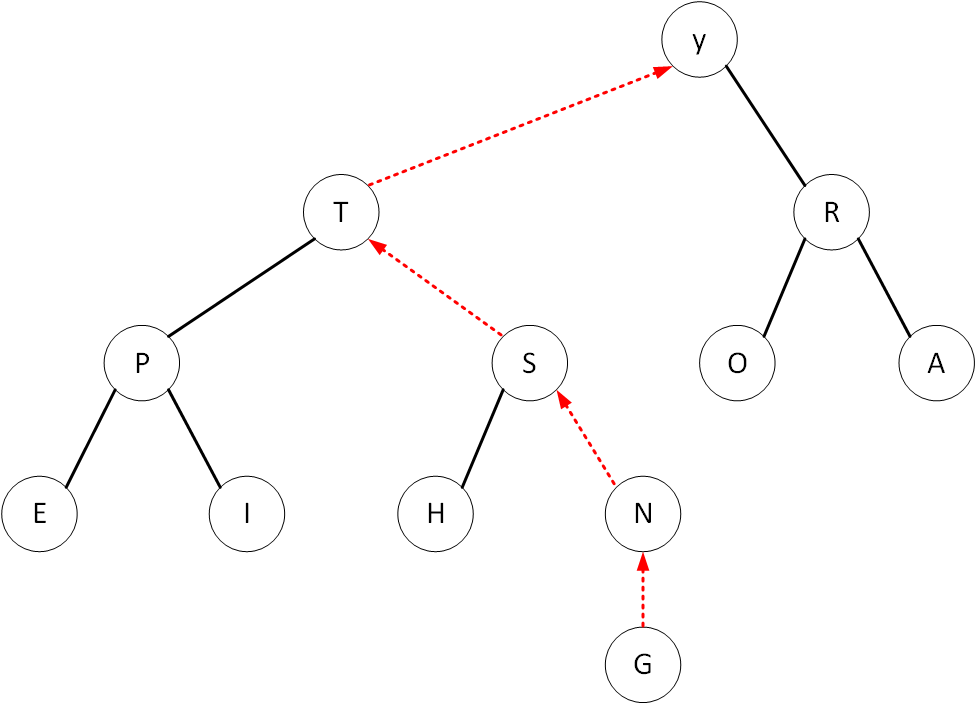
下沉(sink)

当某个元素变得比它的两个子节点或是其中之一小，通过下沉操作来恢复有序状态。例如将堆顶元素”T”删除后再将”G”元素放在原先”T”元素的位置

“G”元素只需要一遍一遍与其子节点进行比较，并交换位置，当”G”元素到达合适的位置时，整个堆就变得有序了

下沉的伪代码

1
2
3
4
5
6
7
8
9
10
11
12
void sink(k)
{
    while (2*k <= N) {
        j = 2*k;
        if ((j<N) &&  less(j, j+1)) 
            j++;
        if (!less(k, j))
            break;
        exch(k, j);
        k = j;
    }
}

自动扩容

由于数组需要在创建时分配固定大小，因此为了提高利用的灵活性，需要队列能够自动调整数组大小。太过频繁的重新调整会增大开销，较为合理的方式是

  • 当数组满时，扩容为原数组2倍

  • 当数组元素大小减小到数组容量时，减小容量为原数组一半

C语言实现MinPQ

MinPQ结构定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* -- MinPQ --{*/
typedef struct _minpq {
    int node_nr;        /* node number */
    int capacity;       /* the capacity of queue */     
    size_t nodesize;    /* every node's size in the queue */   
    int *p;             /* point to the private priority array */
    char *q;            /* point to the node array */
#define MINPQ_F_CDC   0x0001  /* custom define comparator */
#define MINPQ_F_RES   0x0002  /* capacity resize */
    uint16_t flags;
    bool (*comparator)(void *, void *);    /* point to custom define comparator */

    int info_width;     /* use fo debug and dump */
    void (*info_prior_handle)(struct _minpq *, int, char *, int);    /* use fo debug and dump */
    void (*info_value_handle)(struct _minpq *, int, char *, int);    /* use fo debug and dump */
} MinPQ;

创建MinPQ，创建函数需要传入节点大小和容量，如果容量为0，默认支持自动扩容；如果使用自定义优先级，需要传入比较器comparator。创建函数内部会创建并维护一个内部默认的优先级数组p，该数组是整型类型，如果要用默认的整型优先级，后续插入元素时可传入优先级数值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/*
 * Create a Min Priroity Queue(MinPQ)
 *
 * @nodesize: every node's size in the queue
 * @capacity: the capacity of queue
 * @comparator: custom define comparator
 * @flags: queue's features
 *
 * return: MinPQ
 */
MinPQ *MinPQ_create(size_t nodesize, int capacity, 
    bool(*comparator)(void *, void *), uint16_t flags)
{
    int allocnr;

    /* params check */
    if (nodesize <= 0) {log_err("nodesize zero");return NULL;}
    if (capacity < 0) {log_err("capacity invaild");return NULL;}

    MinPQ *q = zalloc(sizeof(MinPQ));
    if (!q) {log_err("MinPQ create error");return NULL;}

    q->node_nr = 0;
    q->nodesize = nodesize;
    q->info_width = 4;

    q->capacity = capacity;
    if (capacity == 0) {    /* if no capacity, we set resize flag auto */
        mask_push(q->flags, MINPQ_F_RES);
    }

    if (comparator != NULL) {
        q->comparator = comparator;
        mask_push(q->flags, MINPQ_F_CDC);
    }

    mask_push(q->flags, flags);

    if (!capacity) {
        allocnr = 1;
    } else {
        allocnr = capacity + 1;
    }

    /* alloc private priority */
    q->p = zalloc(allocnr*sizeof(int));
    q->q = zalloc(allocnr*q->node_nr);

    return q;
}

插入元素，会首先检查容量和是否支持扩容；新节点先放在堆底，然后上浮操作进行有序化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/* 
 * MinPQ insert operation
 * 
 * @q: the queue you want to do insert
 * @u: the node you want to insert
 * @p: the priority of insert node, if use custom define priority, don't need this
 */

err_type MinPQ_insert(struct _minpq *q, void *u, int p)
{
    char *addr;

    if (MinPQ_full(q)) {
        if (mask_exst(q->flags, MINPQ_F_RES)) {
            if (!q->capacity) q->capacity = 1;
            _resize(q, q->capacity*2);
        } else {
            log_err("MinPQ full");
            return et_full;
        }
    }

    q->p[++q->node_nr] = p;
    addr = q->q + q->nodesize*q->node_nr;
    memcpy(addr, u, q->nodesize);
    _swim(q, q->node_nr);
    return et_ok;
}

删除元素，先将堆顶元素拷贝出来，然后将堆底元素移动到堆顶，调用下沉sink进行有序化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
err_type MinPQ_delmin(struct _minpq *q, void *u, int *p)
{
    char *addr1, *addr2;

    if (MinPQ_empty(q)) {
        log_err("MinPQ empty");
        return et_empty;
    }

    addr1 = q->q + q->nodesize;
    memcpy(u, addr1, q->nodesize);
    *p = q->p[1];
    q->p[1] = q->p[q->node_nr];
    addr2 = q->q + q->nodesize*q->node_nr;
    memcpy(addr1, addr2, q->nodesize);
    q->node_nr--;
    _sink(q, 1);
    q->p[q->node_nr+1] = 0;

    if ((q->node_nr>0) && 
        (q->node_nr==(q->capacity-1)/4) &&
        mask_exst(q->flags, MINPQ_F_RES)) {
        _resize(q, q->capacity/2);
    }

    addr2 = q->q + q->nodesize*(q->node_nr+1);
    memset(addr2, 0x0, q->nodesize);
    return et_ok;
}

获取指定索引数据，该函数可以结合for循环遍历队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
err_type MinPQ_get(struct minpq *q, void *u, int *p, int index)
{
    char *addr;

    if (empty(q)) {
        log_err("MinPQ empty");
        return et_empty;
    }

    addr = q->q + q->nodesize*index;
    memcpy(u, addr, q->nodesize);
    *p = q->p[index];
    return et_ok;
}

上浮操作，用到了递归

1
2
3
4
5
6
7
static void _swim(struct _minpq *q, int k)
{
    while ((k>1) && (_greater(q, k/2, k))) {
        _swap(q, k, k/2);
        k = k/2;
    }
}

下沉操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
static void _sink(struct _minpq *q, int k)
{
    int j;

    while (2*k <= q->node_nr) {
        j = 2*k;
        if ((j<q->node_nr) && (_greater(q, j, j+1)))
            j += 1;
        if (!_greater(q, k, j)) 
            break;
        _swap(q, k, j);
        k = j;
    }
}

交换函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
static void _swap(struct __minpq *q, int i, int j)
{
    int tempp;
    char *addr1, *addr2;
    char *tempu = zalloc(q->nodesize);

    tempp = q->p[i];
    q->p[i] = q->p[j];
    q->p[j] = tempp;

    addr1 = q->q + q->nodesize*i;
    addr2 = q->q + q->nodesize*j;
    memcpy(tempu, addr1, q->nodesize);
    memcpy(addr1, addr2, q->nodesize);
    memcpy(addr2, tempu, q->nodesize);
}

比较函数

1
2
3
4
5
6
7
8
9
10
11
12
static bool _greater(struct _minpq *q, int i, int j)
{
    char *addr1, *addr2;

    if (!q->comparator) {
        return (q->p[i] > q->p[j]);
    } else {
        addr1 = q->q + q->nodesize*i;
        addr2 = q->q + q->nodesize*j;
        return q->comparator(addr1, addr2);
    }
}

扩容函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
err_type _resize(struct _minpq *q, int capcaity)
{
    int i;
    char *new;

    if (capcaity <= q->node_nr) {
        log_err("capcaity invaild");
        return et_param;
    }

    new = zalloc(q->nodesize*(capcaity+1));
    if (!new) {
        log_err("alloc new error");
        return et_nomem;
    }

    memcpy(new, q->q, q->nodesize*(q->node_nr+1));
    mem_free(q->q);
    q->q = new;
    q->capacity = capcaity;
    return et_ok;
}

一些辅助查询函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int MinPQ_size(struct _minpq *q)
{
    return (q->node_nr);
}

bool MinPQ_full(struct _minpq *q)
{
    return (q->capacity == q->node_nr);
}

bool MinPQ_empty(struct _minpq *q)
{
    return (q->node_nr == 0);
}