本文基于定制化的TFLite Micro动态链接库,通过”hello world”示例来验证TFLite Micro版本的功能。虽然名字叫是”hello world”,其实并不是在控制台上打印出”hello world”这么简单,而是用Python版本的Tensorflow构建训练一个能够学习并生成正弦波的模型,通过TFLite的转换器转换为.tflite文件,并使用TFLite Micro动态链接库加载并执行推断的过程
开发环境
Inter i5-7200U
Ubuntu18.04.2 x86_64
conda Python3.7虚拟环境
Tensorflow2.1.0
参考
生成数据 首先需要加载一些python库
1 2 3 4 import tensorflow as tfimport numpy as npimport matplotlib.pyplot as pltimport math
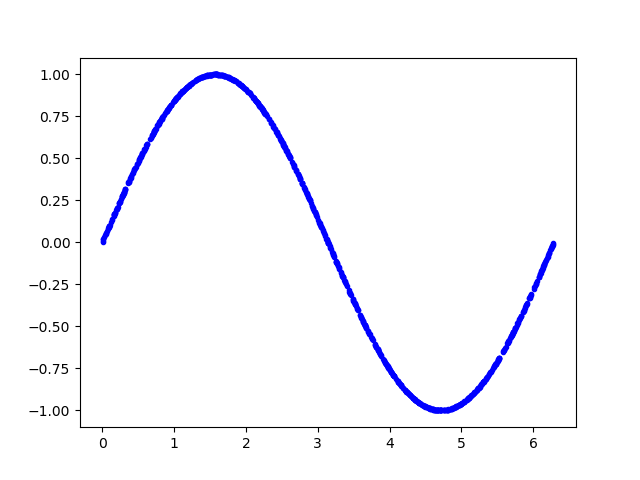
以下代码生成一组随机数,并计算它们的正弦值,并绘图显示
1 2 3 4 5 6 7 SAMPLES = 1000 np.random.seed(1337 ) x_values = np.random.uniform(low=0 , high=2 *math.pi, size=SAMPLES) np.random.shuffle(x_values) y_values = np.sin(x_values) plt.plot(x_values, y_values, 'b.' ) plt.show()
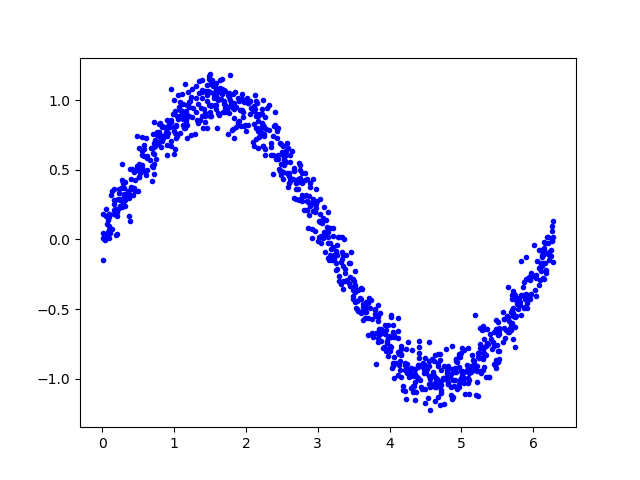
添加噪声 由于数据是由正弦函数直接生成,数据太过平滑。然而现实中获取的各种信号必然夹杂着噪声数据,而机器学习算法能够从带有噪声的数据中学习到真正的信息
为数据添加一些噪声,并绘制显示
1 2 3 y_values += 0.1 * np.random.randn(*y_values.shape) plt.plot(x_values, y_values, 'b.' ) plt.show()
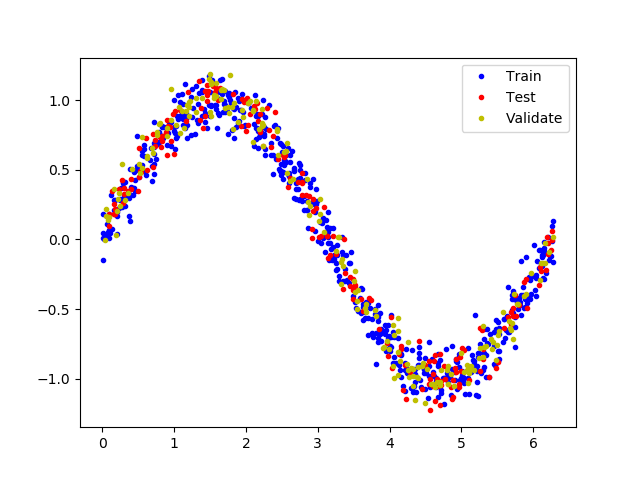
拆分数据 我们已经生成了一个近似真实世界的噪声数据,我们用它来训练模型
为了验证评估模型,以及防止数据的过拟合,我们将数据拆分为训练集、测试集和验证集3部分,比例为3:1:1
以下代码将数据分割,并以不同的颜色显示
1 2 3 4 5 6 7 8 9 TRAIN_SPLIT = int (0.6 * SAMPLES) TEST_SPLIT = int (0.2 * SAMPLES + TRAIN_SPLIT) x_train, x_test, x_validate = np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT]) y_train, y_test, y_validate = np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT]) plt.plot(x_train, y_train, 'b.' , label="Train" ) plt.plot(x_test, y_test, 'r.' , label="Test" ) plt.plot(x_validate, y_validate, 'y.' , label="Validate" ) plt.legend() plt.show()
设计模型 我们将建立一个模型,它接收一个输入,并用它来预测一个输出,此类问题称为回归问题。为了达到这个目的,我们将创建一个简单的神经网络,它将使用多层的神经元来学习数据背后的模式,以便进行预测
首先,我们定义两个层。第一层接收一个输入,并经过16个神经元。输入到来时,每个神经元将根据自身的权重和偏置状态受到不同程度的激活,神经元的激活程度由数字表示。第一层的激活将作为第二层的输入,第二层的输出作为模型的输出值
我们使用Keras来定义模型,模型使用”relu”作为激活函数,优化器使用”rmsprop”,损失函数使用”mse”,使用MAE来评估
1 2 3 4 5 from tensorflow.keras import layersmodel_1 = tf.keras.Sequential() model_1.add(layers.Dense(16 , activation='relu' , input_shape=(1 ,))) model_1.add(layers.Dense(1 )) model_1.compile (optimizer='rmsprop' , loss='mse' , metrics=['mae' ])
训练模型 一旦我们定义好了模型,可以使用数据来训练它。训练过程将x输入到网络中,检查网络输出与原始数据的偏离程度,并调整神经元的偏置和权重。训练过程是在整个数据上多次运行,每次完整的运行都称为”epoch”。在每个”epoch”中,数据以多批次的方式在网络中运行,每一批次都有几个数据进入网络并输出,对网络参数的调整是以一个批次为单位的。”epoch”次数和批次大小都可以通过参数调整
以下代码运行1000个”epoch”,每个批次16个数据,还传递一些数据用于验证。整个训练需要一定的时间
1 2 history_1 = model_1.fit(x_train, y_train, epochs=1000 , batch_size=16 , validation_data=(x_validate, y_validate))
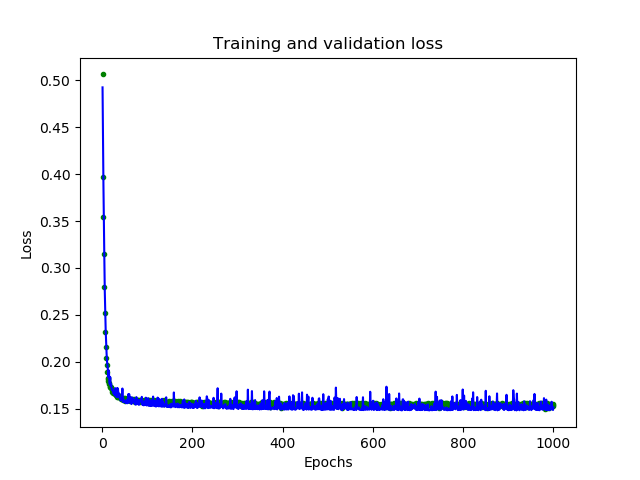
模型评估 在训练期间,模型的性能在数据迭代中不断的提升,训练会生成一个日志,告诉我们性能在训练过程中是如何变化的。以下代码将以图形形式显示其中一些信息
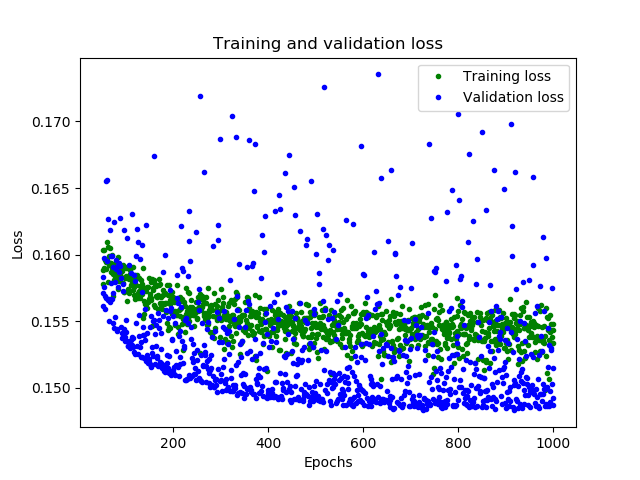
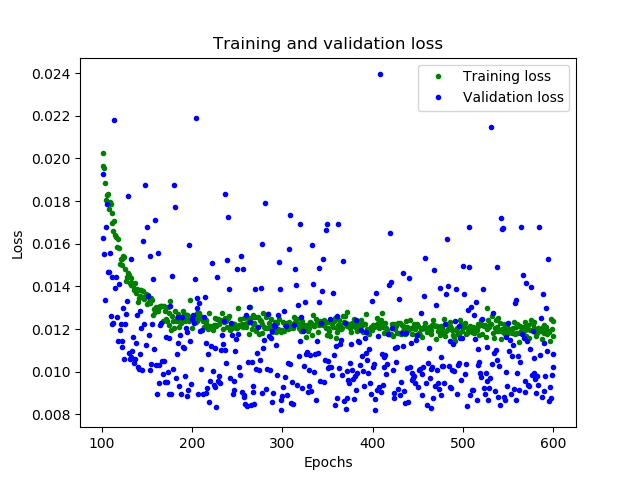
1 2 3 4 5 6 7 8 9 10 loss = history_1.history['loss' ] val_loss = history_1.history['val_loss' ] epochs = range (1 , len (loss) + 1 ) plt.plot(epochs, loss, 'g.' , label='Training loss' ) plt.plot(epochs, val_loss, 'b' , label='Validation loss' ) plt.title('Training and validation loss' ) plt.xlabel('Epochs' ) plt.ylabel('Loss' ) plt.legend() plt.show()
图形中显示了每个epoch的损失函数情况。有多种方式的损失函数,这里我们使用的是均方误差MSE。损失函数在前25个epoch迅速减少,之后趋于平缓,这意味着模型在不断改进。我们的目标是当模型不再改进,或者当训练损失小于验证损失时,意味着学习已经收敛,需要停止训练。为了更清楚的观察平坦部分,我们跳过前50个epoch的训练情况
1 2 3 4 5 6 7 8 SKIP = 50 plt.plot(epochs[SKIP:], loss[SKIP:], 'g.' , label='Training loss' ) plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.' , label='Validation loss' ) plt.title('Training and validation loss' ) plt.xlabel('Epochs' ) plt.ylabel('Loss' ) plt.legend() plt.show()
从上图中可以看出,损失在前600个epoch持续减少,到600之后不再变化,这意味着600之后的训练是没有必要的。同时,我们也可以看到,最低的损失函数值仍然在0.155左右,这意味着我们的网络预测平均偏离了15%。另外,验证损失值跳变很多。为了了解更多模型的性能,我们可以绘制更多数据,这次我们输出MAE平均绝对误差,这是测量网络预测与实际之间差距距离的另一种方法
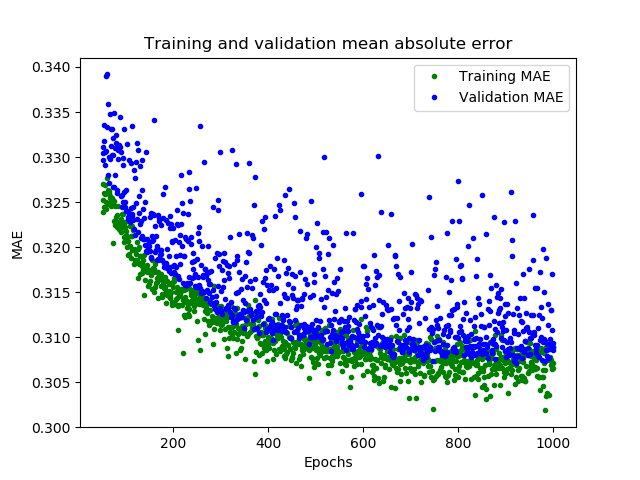
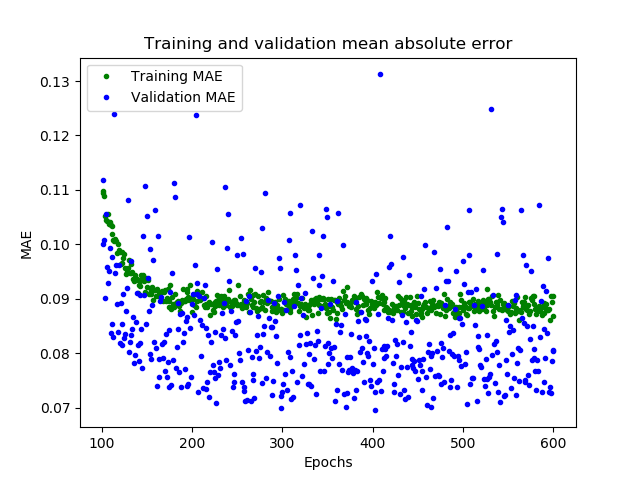
1 2 3 4 5 6 7 8 9 10 plt.clf() mae = history_1.history['mae' ] val_mae = history_1.history['val_mae' ] plt.plot(epochs[SKIP:], mae[SKIP:], 'g.' , label='Training MAE' ) plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.' , label='Validation MAE' ) plt.title('Training and validation mean absolute error' ) plt.xlabel('Epochs' ) plt.ylabel('MAE' ) plt.legend() plt.show()
这幅图告诉了我们更多的信息。训练数据的MAE始终低于验证数据的MAE,这意味着网络可能有过拟合,或者学习训练数据太僵硬,以至于无法对新数据做出有效预测。此外,MAE整体都较高,最多为0.305,这表明模型的预测有30%的偏差。为了更清楚的了解到发生了什么,我们可以将网络预测值和实际训练值进行比较
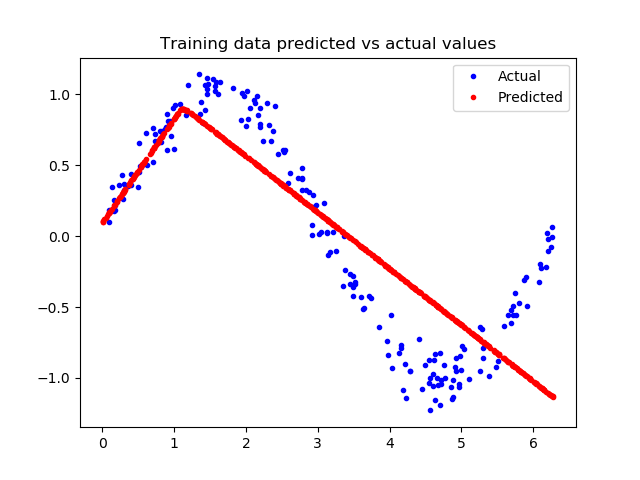
1 2 3 4 5 6 7 predictions = model_1.predict(x_train) plt.clf() plt.title('Training data predicted vs actual values' ) plt.plot(x_test, y_test, 'b.' , label='Actual' ) plt.plot(x_train, predictions, 'r.' , label='Predicted' ) plt.legend() plt.show()
这张图表明网络已经学会以非常有限的方式逼近正弦函数,但是这是一个线性的逼近。这种拟合的刚性表明,该模型没有足够的能力来学习正弦波函数的全部复杂性,因此只能用过于简单的方法来近似它。我们可以修改模型,来改进性能
改变模型 再增加一层神经元,以下增加一个16个神经元的层
1 2 3 4 5 model_2 = tf.keras.Sequential() model_2.add(layers.Dense(16 , activation='relu' , input_shape=(1 ,))) model_2.add(layers.Dense(16 , activation='relu' )) model_2.add(layers.Dense(1 )) model_2.compile (optimizer='rmsprop' , loss='mse' , metrics=['mae' ])
我们现在将训练新模型。为了节省时间,我们只训练600个epoch
1 2 history_2 = model_2.fit(x_train, y_train, epochs=600 , batch_size=16 , validation_data=(x_validate, y_validate))
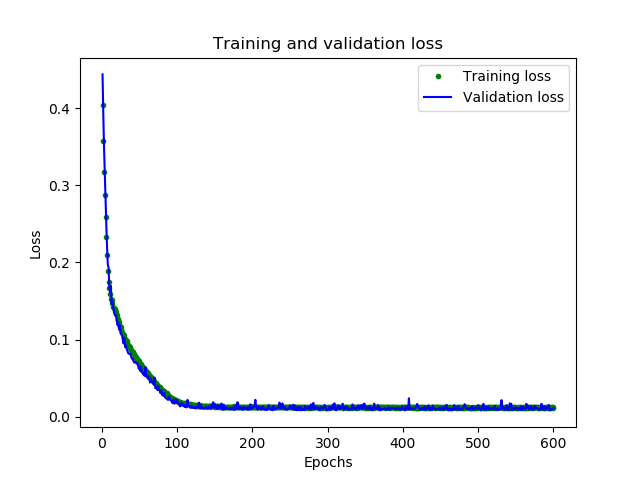
再次评估模型 可以看到,模型已经有了很大改进,验证损失从0.15降到0.015,验证MAE从0.31降低到0.1
以下代码显示新模型训练的情况
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 loss = history_2.history['loss' ] val_loss = history_2.history['val_loss' ] epochs = range (1 , len (loss) + 1 ) plt.plot(epochs, loss, 'g.' , label='Training loss' ) plt.plot(epochs, val_loss, 'b' , label='Validation loss' ) plt.title('Training and validation loss' ) plt.xlabel('Epochs' ) plt.ylabel('Loss' ) plt.legend() plt.show() SKIP = 100 plt.clf() plt.plot(epochs[SKIP:], loss[SKIP:], 'g.' , label='Training loss' ) plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.' , label='Validation loss' ) plt.title('Training and validation loss' ) plt.xlabel('Epochs' ) plt.ylabel('Loss' ) plt.legend() plt.show() plt.clf() mae = history_2.history['mae' ] val_mae = history_2.history['val_mae' ] plt.plot(epochs[SKIP:], mae[SKIP:], 'g.' , label='Training MAE' ) plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.' , label='Validation MAE' ) plt.title('Training and validation mean absolute error' ) plt.xlabel('Epochs' ) plt.show()
很好的结果,从图中可以看到一些令人兴奋的事情
让我们对照模型的预测值和训练数据
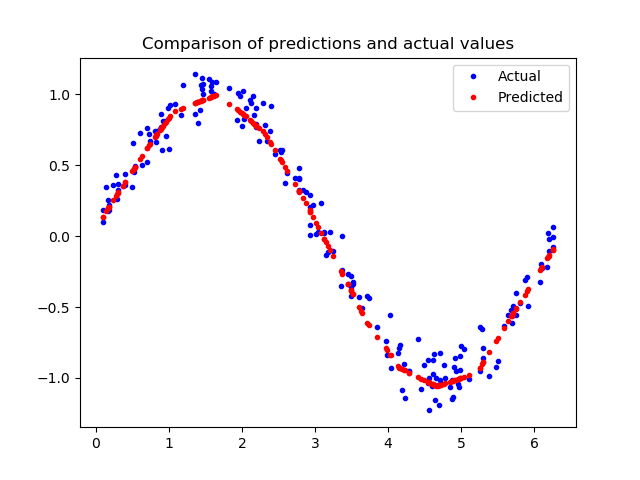
1 2 3 4 5 6 7 8 loss = model_2.evaluate(x_test, y_test) predictions = model_2.predict(x_test) plt.clf() plt.title('Comparison of predictions and actual values' ) plt.plot(x_test, y_test, 'b.' , label='Actual' ) plt.plot(x_test, predictions, 'r.' , label='Predicted' ) plt.legend() plt.show()
由上图看出,预测结果与我们的数据非常吻合。这个模型并不完美,它的预测并没有形成一个平滑的正弦曲线,如果我们想更进一步,我们可以尝试进一步增加模型的容量,也许可以使用一些技术来防止过度拟合。然而,机器学习的一个重要部分是知道什么时候停止,这个模型对于我们示例来说已经足够好了
转换模型到TFLite 将模型用于TFLite微控制器,需要将其转换为正确的格式,为此我们将使用Tensorflow Lite转换器,转换器可以以一种特殊的、节省空间的格式将模型输出到文件。由于是部署到微控制器上,我们希望它尽可能小,可以通过量化的方法减小尺寸。它降低了模型权重的精度,以节省内存。因为量化模型更小,因此运行起来也更快
转换器可以在转换时选择是否进行量化
1 2 3 4 5 6 7 8 9 converter = tf.lite.TFLiteConverter.from_keras_model(model_2) tflite_model = converter.convert() open ("sine_model.tflite" , "wb" ).write(tflite_model)converter = tf.lite.TFLiteConverter.from_keras_model(model_2) converter.optimizations = [tf.lite.Optimize.OPTIMIZE_FOR_SIZE] tflite_model = converter.convert() open ("sine_model_quantized.tflite" , "wb" ).write(tflite_model)
执行以上代码可以看到,未量化的模型大小为2732KB,量化模型大小为2720KB
测试转换后的模型 为了证明这些模型在转换和量化之后仍然是准确的,我们将使用这两个模型进行预测,并将其与我们的测试结果进行比较:
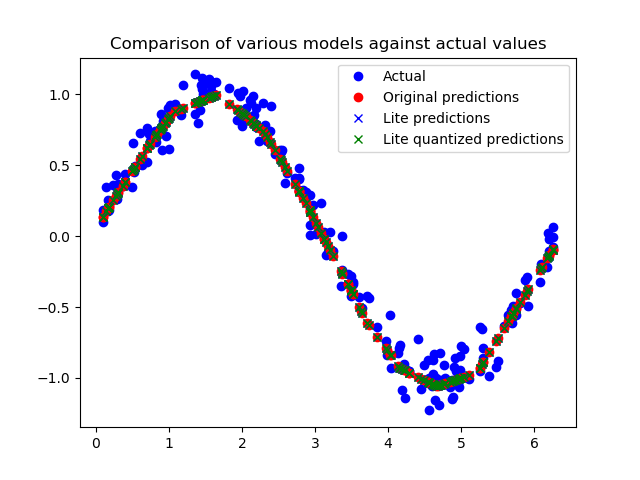
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 sine_model = tf.lite.Interpreter('sine_model.tflite' ) sine_model_quantized = tf.lite.Interpreter('sine_model_quantized.tflite' ) sine_model.allocate_tensors() sine_model_quantized.allocate_tensors() sine_model_input = sine_model.tensor(sine_model.get_input_details()[0 ]["index" ]) sine_model_output = sine_model.tensor(sine_model.get_output_details()[0 ]["index" ]) sine_model_quantized_input = sine_model_quantized.tensor(sine_model_quantized.get_input_details()[0 ]["index" ]) sine_model_quantized_output = sine_model_quantized.tensor(sine_model_quantized.get_output_details()[0 ]["index" ]) sine_model_predictions = np.empty(x_test.size) sine_model_quantized_predictions = np.empty(x_test.size) for i in range (x_test.size): sine_model_input().fill(x_test[i]) sine_model.invoke() sine_model_predictions[i] = sine_model_output()[0 ] sine_model_quantized_input().fill(x_test[i]) sine_model_quantized.invoke() sine_model_quantized_predictions[i] = sine_model_quantized_output()[0 ] plt.clf() plt.title('Comparison of various models against actual values' ) plt.plot(x_test, y_test, 'bo' , label='Actual' ) plt.plot(x_test, predictions, 'ro' , label='Original predictions' ) plt.plot(x_test, sine_model_predictions, 'bx' , label='Lite predictions' ) plt.plot(x_test, sine_model_quantized_predictions, 'gx' , label='Lite quantized predictions' ) plt.legend() plt.show()
从图中我们可以看出,对原始模型、转换模型和量化模型的预测都非常接近,无法区分。这意味着我们的量化模型已经可以使用了!
使用C++程序执行推断 这里使用C++程序需要依赖TFLite Micro动态链接库,参见
通过xxd命令将模型文件转换为C++源文件
1 xxd -i sine_model_quantized.tflite > sine_model_quantized.cc
可以看到生成的C++文件中,模型是以字节序列存放的,并通过sine_model_quantized.h文件向外暴露模型地址和长度
1 2 3 4 5 6 7 unsigned char sine_model_quantized_tflite[] = { 0x18 , 0x00 , 0x00 , 0x00 , 0x54 , 0x46 , 0x4c , 0x33 , 0x00 , 0x00 , 0x0e , 0x00 , 0x18 , 0x00 , 0x04 , 0x00 , 0x08 , 0x00 , 0x0c , 0x00 , 0x10 , 0x00 , 0x14 , 0x00 , ...... } unsigned int sine_model_quantized_tflite_len = 2640 ;
我们创建一个main.cc源文件,用来加载模型并循环执行推断,将模型输出导出到csv文件中,最后用python绘图呈现模型的预测效果
引用一些头文件 TFLite Micro程序需要引用一些必要的头文件
1 2 3 4 5 6 7 8 9 10 11 12 #include "tensorflow/lite/micro/kernels/all_ops_resolver.h" #include "tensorflow/lite/micro/micro_error_reporter.h" #include "tensorflow/lite/micro/micro_interpreter.h" #include "tensorflow/lite/micro/debug_log.h" #include "tensorlfow/lite/version.h" #include "sine_model_data.h" #include <iostream> #include <fstream> #include <sstream> using namespace std;
all_ops_resolver.h文件中定义了一些优化器相关的运算组建,例如全连接(Full Connected, FC)、柔性最大化函数Softmax、卷积conv
micro_error_reporter.h文件中定义了调试方法
micro_interpreter.h文件中是解释器的定义
sin_model_data.h引用模型文件
加载模型 首先创建一个调试器reporter
1 2 tflite::MicroErrorReporter micro_error_reporter; tflite::ErrorReporter* error_reporter = & micro_error_reporter;
调用GetModel()方法加载模型
1 2 3 4 5 6 7 8 const tflite::Model* model = ::tflite::GetModel (g_sine_model_data);if (model->version () != TFLITE_SCHEMA_VERSION) { error_reporter->Report ( "Model provided is schema version %d not equal " "to supported version %d.\n" , model->version (), TFLITE_SCHEMA_VERSION); return 0 ; }
创建一个运算器
1 tflite::ops::micro::AllOpsResolver resolver;
创建解释器,并为模型推断分配内存空间
1 2 3 4 5 6 7 8 9 10 const int tensor_arena_size = 10 * 1024 ;uint8_t tensor_arena[tensor_arena_size];tflite::MicroInterpreter interpreter (model, resolver,tensor_arena, tensor_arena_size, error_reporter) TfLiteStatus alloc_status = interpreter.AllocateTensors (); if (alloc_status != kTfLiteOk) { error_reporter->Report ("Alloc tensors Error:%d" , alloc_status); return 0 ; }
创建指针指向模型输入和输出
1 2 3 tflite::MicroInterpreter *inter = &interpreter; TfLiteTensor* input = interpreter.input (0 ); TfLiteTensor* output = interpreter.output (0 );
创建csv文件”data.csv”
1 2 ofstream outFile; outFile.open ("data.csv" , ios::out);
以下循环,产生1000个输入,执行模型推断,并将输入和输出保存到csv文件,并打印到屏幕
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 int kInferencesPerCycle = 1000 ; const float kXrange = 2.f * 3.14159265359f ; int inference_count = 0 ;while (true ) { float position = static_cast <float >(inference_count) / static_cast <float >(kInferencesPerCycle); float x_val = position * kXrange; input->data.f[0 ] = x_val; TfLiteStatus invoke_status = inter->Invoke (); if (invoke_status != kTfLiteOk) { error_reporter->Report ("Invoke Error:%d" , invoke_status); return 0 ; } float y_val = output->data.f[0 ]; printf ("x:%f, y:%f\r\n" ,x_val, y_val); outFile<<x_val<<',' <<y_val<<endl; inference_count += 1 ; if (inference_count >= kInferencesPerCycle) break ; } outFile.close ();
运行结果 编译程序并运行,数据保存到了”data.csv”文件中,查看其内容
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 cat data.csv | head -n 20 0,0.0486171 0.00628319,0.0537117 0.0125664,0.0588063 0.0188496,0.0639008 0.0251327,0.0689952 0.0314159,0.0740901 0.0376991,0.0791845 0.0439823,0.0842792 0.0502655,0.0893737 0.0565487,0.0944682 0.0628319,0.0995628 0.069115,0.104657 0.0753982,0.109752 0.0816814,0.114847 0.0879646,0.119941 0.0942478,0.125036 0.100531,0.13013 0.106814,0.135225 0.113097,0.14032 0.119381,0.145414
编写python脚本draw.py读取data.csv文件并将数值绘制出来
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import matplotlib.pyplot as pltimport csvX = [] Y = [] with open ('data.csv' ,'r' ) as myFile: lines=csv.reader(myFile) for line in lines: x = float (line[0 ]) y = float (line[1 ]) X.append(x) Y.append(y) plt.plot(X, Y) plt.show()
执行脚本
结果如图
可见模型输出的结果准确